Canvas и JavaScript. Кривые

В canvas можно нарисовать квадратичную кривую и кривую Безье. Скоро вы узнаете, что отличает эти кривые друг от друга, прочитав статью до конца.
Квадратичная кривая
Для рисования квадратичной кривой в canvas используется метод quadraticCurveTo(). Сделаем необходимую заготовку из HTML / CSS кода.
<canvas id="curve" width="600" height="300"></canvas>
#curve {
width: 600px;
height: 300px;
margin: 40px;
background-image: url(grid.png);
}
Квадратичная кривая состоит из координат начальной точки, точки искривления и конечной точки.
Принцип построения квадратичной кривой
let canvas = document.getElementById('curve');
let ctx = canvas.getContext('2d');
ctx.beginPath(); // начало нового пути
ctx.lineWidth = 7; // толщина обводки
ctx.strokeStyle="green"; // цвет обводки
ctx.moveTo(75, 150); // координаты начальной точки
ctx.quadraticCurveTo(150, 0, 300, 150); // координаты точки искривления и конечной точки
ctx.stroke(); // команда обводки
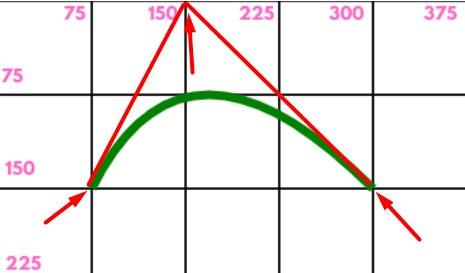
Пример квадратичной кривой
let canvas = document.getElementById('curve');
let ctx = canvas.getContext('2d');
ctx.beginPath();// начало нового пути
ctx.lineWidth = 7; // толщина обводки
ctx.strokeStyle="green"; // цвет обводки
ctx.moveTo(75, 75); // координаты начальной точки
ctx.quadraticCurveTo(100, 150, 300, 50); // координаты точки искривления и конечной точки
ctx.stroke();

Кривая Безье
Кривая Безье строит не одну точку искривления, а две точки. Исходя из того, что у одной точки две координаты (X,Y), то для построения двух точек искривления потребуется четыре координаты. Эта особенность позволяет построить более сложную кривизну и отличает ее от квадратичной кривой. Для создания кривой Безье, воспользуемся методом bezierCurveTo().
Принцип построения кривой Безье
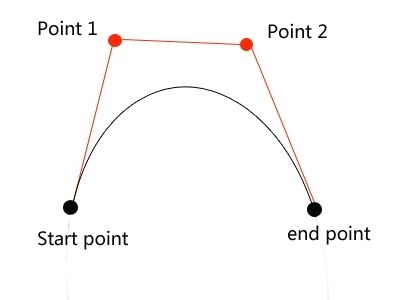
Пример кривой Безье
let canvas = document.getElementById('curve');
let ctx = canvas.getContext('2d');
ctx.beginPath();// начало нового пути
ctx.lineWidth = 7; // толщина обводки
ctx.strokeStyle="green"; // цвет обводки
ctx.moveTo(100, 150); // координаты начальной точки
ctx.bezierCurveTo(150, 50, 340, 10, 400, 200); // координаты точки искривления и конечной точки
ctx.stroke();

Пример рисования фигуры сердце
let canvas = document.getElementById('curve');
let ctx = canvas.getContext('2d');
ctx.beginPath();
ctx.fillStyle="red"; // цвет заливки
ctx.moveTo(75, 40);
ctx.bezierCurveTo(75, 37, 70, 25, 50, 25);
ctx.bezierCurveTo(20, 25, 20, 62.5, 20, 62.5);
ctx.bezierCurveTo(20, 80, 40, 102, 75, 120);
ctx.bezierCurveTo(110, 102, 130, 80, 130, 62.5);
ctx.bezierCurveTo(130, 62.5, 130, 25, 100, 25);
ctx.bezierCurveTo(85, 25, 75, 37, 75, 40);
ctx.fill();

Итоги
Квадратичная кривая строится с помощью трех точек, что эквивалентно шести координатам. Для создания кривой Безье надо задать четыре точки (8 координат), большее количество точек обеспечивает более плавный переход между ними.
-
Создано 17.05.2021 10:33:48

-
 Михаил Русаков
Михаил Русаков






Комментарии (0):
Для добавления комментариев надо войти в систему.
Если Вы ещё не зарегистрированы на сайте, то сначала зарегистрируйтесь.